[ paper study automl ]

심층 피처 합성: 데이터 과학 노력의 자동화를 위하여

원문: Deep Feature Synthesis : Towards Automating Data Science Endeavors (2015 년)

나의 생각

최근 AutoML이 화두로 떠오르고 있지만, 초모수 최적화 (Hyper-parameter Optimization)나 전이 학습 (Transfer Learning), 그리고 신경망 구성 검색(Neural Architecture Search) 등의 최신 분야 중심으로 연구가 진행되고 있습니다. 2015 년에 발표된 이 논문은 시간이 좀 지나긴 했지만, 전통적인 기계 학습에서 꼭 필요한 피처 엔지니어링 (Feature Engineering)을 자동화할 수 있는 아이디어를 제시합니다.

또한 저자들은 이 아이디어를 Featuretools 라는 파이썬 프레임웍으로 구현해 제공하고 있습니다. 논문에서 제안하듯, 보조적으로만 활용하더라도 데이터 과학자의 문제풀이 시간을 단축시켜 주는 좋은 방법이 될 것으로 기대합니다. 이 연구에서 초모수 최적화에 사용된 코퓰라(Copula) 프로세스는 본문의 내용만으로는 이해하기 어려워, 따로 살펴보아야 할 것 같습니다.

주의

이글은 좋은 논문을 소개하기 위해 핵심 내용 중심으로 번역한 것입니다.
번역에 누락이나 오류가 있을 수 있으니, 정확한 내용은 꼭 원문을 참고하시기 바랍니다.

초록 - 본 논문에서는 원시 데이터에서 예측 모델을 자동으로 도출할 수 있는 ‘데이터 과학 머신’을 개발합니다. 이 자동화를 달성하기 위해 먼저 관계형 데이터 세트의 피처를 자동으로 생성하기 위한 ‘심층 피처 합성(Deep Feature Synthesis)’ 알고리즘을 제안하고 개발합니다. 알고리즘은 데이터의 기본 필드에 대한 관계를 따른 다음, 해당 경로를 따라 수학적 함수를 순차적으로 적용하여 최종 피처를 만듭니다. 두 번째로, 일반화 가능한 기계 학습 파이프 라인을 구현하고 새로운 가우시안 코퓰라 프로세스 기반 접근 방식을 사용하여 튜닝합니다. 우리는 906 개의 다른 데이터 과학 팀이 참여한 3 개의 데이터 과학 경진 대회에 데이터 과학 머신(Data Science Machine)을 참여 시켰습니다. 우리의 접근 방식은 이 대회에서 615 개 팀을 능가했습니다. 3 번의 대회 중 두 번은 대다수의 경쟁자를 이겼으며, 세 번째는 최고 경쟁자 점수의 94 %를 달성했습니다. 최선의 경우, 우리는 진행중인 대회에서 전체 팀의 85.6 %를 이기고 최고 제출 점수의 95.7 %를 달성했습니다.

I. 소개

데이터 과학은 데이터에서 통찰력, 지식 및 예측 모델을 도출하는 것으로 구성됩니다. 이 노력의 한쪽 끝에는 데이터 청소와 큐레이션, 다른 쪽 끝에는 결과의 전파가 있으며, 데이터 수집 및 동기화도 포함될 수 있습니다. 그간의 데이터를 효율적으로 저장, 검색 및 처리할 수 있는 시스템 및 소프트웨어의 성공적인 개발과 확산 이후, 이제는 예측 및 상관 분석으로 관심이 옮겨졌습니다. 우리의 목표는 이러한 노력을 보다 효율적이고 즐겁고 성공적으로 만드는 것입니다.

먼저, 우리는 KAGGLE에서 발표한 것과 같은 많은 데이터 과학 문제와 컨퍼런스 내 경진대회 (KDD 컵, IJCAI, ECML) 같은 많은 데이터 과학 문제가 몇 가지 공통된 속성을 가지고 있음을 발견했습니다. 첫째, 데이터는 구조적이고 관계적이며 일반적으로 관계형 링크가 있는 테이블 세트로 표시됩니다. 둘째, 데이터는 복잡한 시스템과 인간 사이 상호작용의 일부 측면을 포착합니다. 셋째, 제시된 문제는 인간의 행동, 의사 결정 또는 활동의 일부 측면을 예측하려고 시도합니다 (예 : 판매 후 고객이 다시 구매할지 여부 [IJCAI], 프로젝트가 기부자에 의해 자금을 지원 받을지 여부 예측 [KDD Cup 2014], 또는 택시 기사가 갈 수있는 곳 [ECML]).

예측 문제가 주어지면, 데이터 과학자는 먼저 피처(Feature)로 알려진 변수를 만들어야 합니다. 데이터 과학자는 테이블에서 일부 정적 필드 (예 : 성별, 연령 등) 를 피처로 사용하여 시작한 다음, 직감을 통해 결과를 예측할 수 있을 것 같은 특화된 피처를 구성할 수 있습니다. 다음으로 과학자는 원시 필드를 다른 척도 값으로 변환하는 새로운 피처를 개발할 수 있습니다 (예 : “어떤 피처의 백분위수”). 이것은 그림 1의 첫 세 블록에 설명되어 있습니다.

그림 1

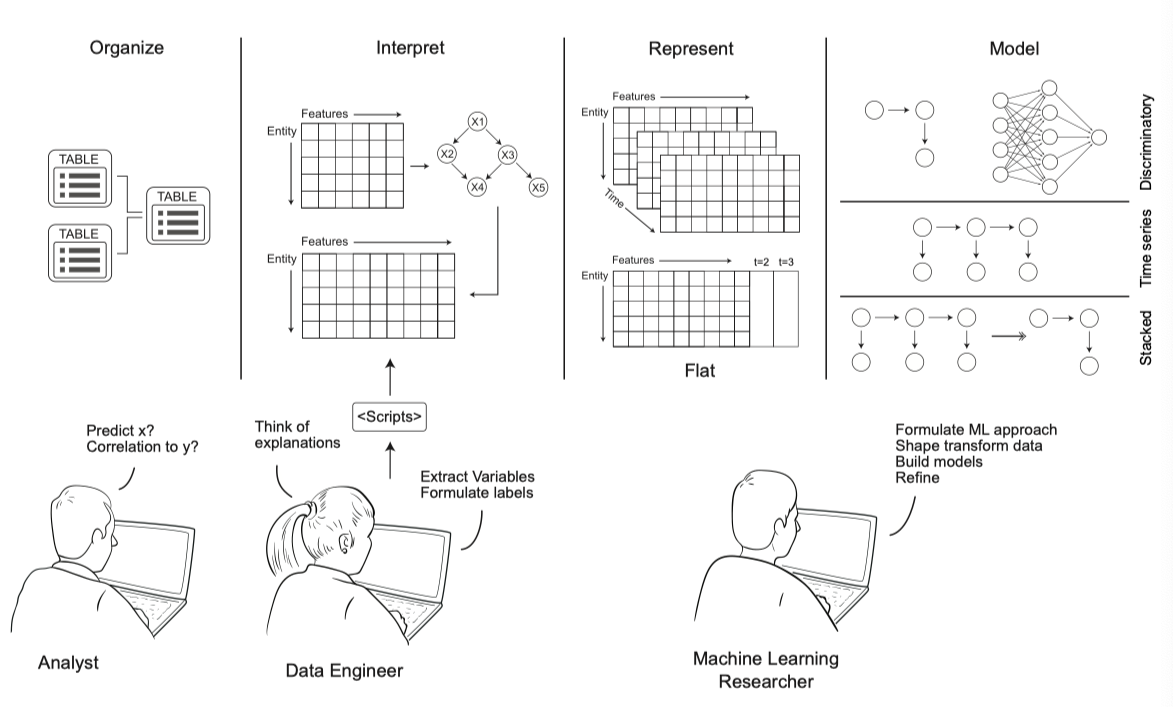
그림 1. 전형적인 데이터 과학 노력. 분석가는 질문을 제기하면서 시작합니다: x 또는 y 가 z 와 상관되어 있는지 예측할 수 있습니까? 이러한 질문은 일반적으로 데이터를 보유한 비즈니스 또는 연구원의 요구에 따라 정의됩니다. 둘째, 예측 문제가 주어지면 데이터 엔지니어는 설명 변수를 가정하고, 해당 변수를 추출하는 스크립트를 작성합니다. 이러한 변수 / 피처 및 표현을 고려하여 기계 학습 연구자는 주어진 예측 목표에 대한 모델을 작성하고, 다양한 모델링 기술을 적용합니다. 현재 예측 문제에 대한 가장 일반적인 방법을 식별하기 위해, 모델링 방법의 공간 내에서 선택을 합니다. 데이터 과학자는 모델을 작성, 개선 및 검증하기 위해 질문을 가정하고 변수를 형성하는 전체 과정을 수행할 수 있습니다.

II. 심층 피처 합성

심층 피처 합성 (Deep Feature Synthesis) 은 관계형 데이터 세트에 대한 피처를 자동으로 생성하는 알고리즘입니다. 이 알고리즘은 기본적으로 데이터의 기본 필드에 대한 관계를 따른 다음, 최종 피처를 만들기 위해 해당 경로를 따라 수학 함수를 순차적으로 적용합니다. 계산을 순차적으로 쌓아가면서, 우리는 각각의 새 피처가 특정 깊이 $d$를 갖는 것으로 정의할 수 있다는 것을 알았습니다. 따라서 우리는 알고리즘을 심층 피처 학습 이라고 부릅니다. 이 섹션에서는 심층 피처 학습의 동기를 설명하고, 피처 합성 추상화를 정의하고, 알고리즘을 제시합니다.

A. 프로토타입 문제와 동기

전자상거래 웹 사이트에 대한 가상의 데이터 세트를 고려해 봅시다. 우리의 목표는 사용 가능한 모든 데이터를 기반으로 고객의 행동을 설명하는 피처를 계산하는 것입니다. 이 데이터 세트의 스키마는 그림 2에 표시되어 있습니다.

그림 2

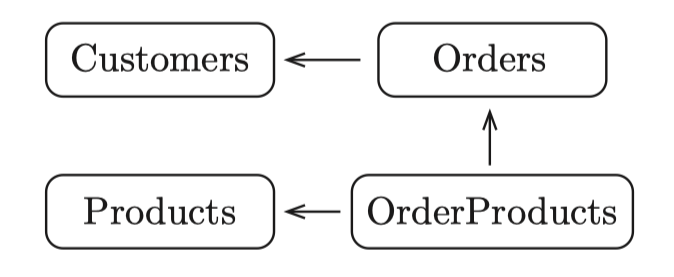
그림 2. 전자상거래 웹 사이트를 위한 단순화된 스키마. 4 개의 엔터티가 있습니다. 한 엔터티에서 다른 엔터티로의 화살표는 데이터베이스에서 첫 번째 엔터티가 두 번째 엔터티를 참조함을 나타냅니다.

데이터 과학자처럼 생각하기 위해, 우리는 고객을 설명하는 피처 (예 : “고객이 얼마나 자주 구매합니까?” 또는 “고객이 마지막으로 구매 한 후 얼마나 되었습니까?”)으로 번역될 수 있는 질문을 하는 것으로 시작할 수 있습니다. 또한 고객과 관련된 엔터티를 보고 이에 대해 질문할 수도 있습니다 (예 : “고객의 총 주문 가격은 얼마입니까?” 또는 “이 고객은 일반적으로 고급 또는 저렴한 제품을 구매합니까?”). 관계를 따르고, 값을 집계하고, 새 피처를 계산하는 것을 통해 이러한 질문을 피처로 변환할 수 있습니다. 우리의 목표는 이러한 유형의 피처를 생성하거나, 프록시 수량으로 동작할 수 있는 계산을 생성하는 알고리즘을 설계하는 것입니다.

B. 피처 합성 추상화

심층 피처 합성의 입력은 상호 연결된 엔터티의 집합 및 그것과 연관된 테이블입니다. 테이블에 있는 엔터티의 각 인스턴스마다 고유한 식별자가 있습니다. 선택적으로 엔터티는 고유 식별자를 사용하여 관련 엔터티의 인스턴스를 참조할 수 있습니다. 엔터티의 인스턴스에는 숫자(numeric), 범주형(categorical), 타임 스탬프(timestamp) 및 자유 텍스트(freetext) 타입 중 하나에 해당하는 피처가 있습니다.

주어진 데이터 세트의 표기 측면에서, 우리는 $E^{(1 \dotso K)}$로 엔터티를 나타냅니다. 여기서 각 엔터티 테이블은 $1 \dotso J$ 피처를 가집니다. 특정 항목을 $x^k_{i, j}$로 표시하는데, 이는 $k$ 번째 엔터티의 $i$ 번째 인스턴스에 대한 피처 $j$의 값입니다.

다음으로 우리는 주어진 엔터티와 그것의 데이터 테이블 및 관계에 대해, 엔터티 와 관계 의 두 가지 레벨로 적용되는 여러 수학 함수를 정의합니다. 아래에서 이 함수들을 살펴보겠습니다. 피처 조립의 대상인 엔터티 $E^k$를 생각해 봅시다. 표기상의 편의를 위해 특정 엔터티를 나타내는 데 사용되는 $k$ 는 생략하겠습니다.

첫 번째 피처 세트는 엔터티 $k$ 에만 해당하는 테이블의 피처 및 그 값을 고려하여 계산됩니다. 이것을 엔터티 피처 이라고 하며 아래에 설명합니다.

엔터티 피처 (efeat) : 엔터티 피처는 각 항목 $x_{i,j}$의 값을 계산하여 유도합니다. 이 피처는 배열 $x_{:,j}$에 요소별로 적용된 계산 함수를 기반으로 할수 있습니다. 예를 들어 범주형 문자열 데이터 유형을 사전 결정된 고유 숫자 값으로 변환하거나, 숫자 값의 반올림처럼 엔터티 테이블의 기존 피처를 다른 타입의 값으로 변환하는 함수가 있습니다. 다른 예로는 타임 스탬프를 주중일(weekday) (1-7), 월중일(day of the month) (1-30 / 31), 연중월(month of the year) (1-12) 또는 일중시(hour of the day) (1-24)의 4 가지 피처로 변환하는 것이 있습니다.

이러한 피처에는 $j$ 번째 피처, $x_{:, j}$ 및 다음 식으로 주어지는 $x_{i,j}$ 을 위해, 전체 값 세트에 함수를 적용하는 것도 포함됩니다.

식 1

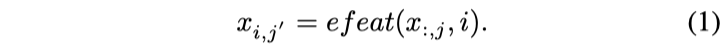
이러한 계산의 예로는 누적 분포 함수 (cdf) 기반 피처가 있습니다. 이 피처를 생성하기 위해 $x_{:,j}$ 에 대한 밀도 함수를 만들고, $x_{i,j}$ (또는 백분위수)의 누적 밀도 값을 평가하여 새로운 피처를 형성합니다.

두 번째 피처 세트는 두 개의 관련 엔터티 $E^l$ 및 $E^k$ 를 결합 분석하여 유도됩니다. 이 두 엔터티는 순방향(forward) 또는 역방향(backward) 의 두 가지 방법 중 하나로 서로 연관됩니다.

순방향 : 순방향 관계는 엔터티 $E^l$의 인스턴스 $m$ 과 다른 엔터티 $E^k$의 $i$ 단일 인스턴스 사이에 있습니다. $i$ 가 $m$ 에 대한 명시적인 의존성이 있기 때문에, 이것은 순방향 관계로 간주됩니다. 위의 전자상거래 예에서, Orders 엔터티는 Customers 와 순방향 관계를 갖습니다. 즉, Orders 테이블의 각 주문은 한 고객과만 관련이 있습니다.

역방향 : 역방향 관계는 $E^k$의 인스턴스 $i$ 에서 순방향 관계를 갖는 $E^l$ 의 모든 인스턴스 $m = {1\dotso M}$ 로의 관계입니다. 위와 같은 예에서 Customers 엔터티는 Orders 와 역방향 관계가 있습니다. 즉, 많은 주문이 동일한 고객을 가리킬 수 있습니다.

직접 피처 (dfeat) : 직접 피처는 순방향 관계에 적용됩니다. 여기에서, 관련 엔터티 $i \in E^k$의 피처는 $m \in E^l$에 대한 피처로 직접 전이됩니다.

관계형 피처 (rfeat) : 관계형 피처는 역방향 관계에 적용됩니다. 그것들은 관련 엔터티 $E^l$의 피처 $j$ 에 대한 값의 모음이며, $E^k$의 식별자가 $e^k = i$ 인 엔터티 $E^l$ 의 피처 $j$ 의 모든 값을 추출하여 만들어진 $x^l_{:,j \vert e^k=i}$ 에 수학 함수를 적용하여, 엔터티 $E^k$의 인스턴스 $i$ 에 대해 유도됩니다.

식 2

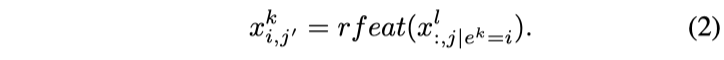
rfeat 함수의 일부 예는 min, max 및 count 입니다. 다른 rfeat 함수는 $x^l_{:,j \vert e^k=i}$ 에 대한 확률 밀도 함수에 적용될 수 있는 함수를 포함합니다.

C. 심층 피처 합성 알고리즘

심층 피처 합성 알고리즘을 설명하기 위해 먼저 $E^{1 \dotso K}$로 표시된 $K$ 엔터티의 데이터 세트를 고려합니다. 우리의 목표는 타겟 $E^k $ 에 대한 rfeat, dfeat 및 efeat 함수를 추출하는 것입니다. 또한 우리는 $E^k$가 순방향 또는 역방향 관계를 갖는 모든 엔터티를 알고 있는데, 이들은 세트 $E_F$ 및 $E_B$로 표시됩니다.

먼저, efeat 피처는 엔터티 내에 이미 존재하는 피처를 사용하여 작성되는 것을 알 수 있습니다. rfeat 및 dfeat 피처를 먼저 합성해야, 결과에 efeat 피처를 적용할 수 있습니다. $E^k$ 에 대한 rfeat 피처를 생성하기 위해 $E_B$의 엔터티 피처를 사용합니다. 따라서 우리는 $E^k$ 의 rfeat 피처를 실현하기 전에 $E^B$ 의 각 엔터티에 대한 모든 피처 타입을 만들어야 합니다. 비슷한 식으로 $E^k$에 dfeat 피처를 추가합니다. 이 피처는 $E_F$ 엔터티의 피처를 사용하여 실현되므로 $E_F$의 각 엔터티에 대한 모든 피처를 먼저 계산해야 합니다. 마지막으로, 모든 rfeat 및 dfeat 피처가 $E^k$에 추가되면 efeat 피처를 생성할 수 있습니다. 그림 3은 각 피처 유형을 올바르게 생성하기 위한 계산 순서를 보여줍니다.

그림 3

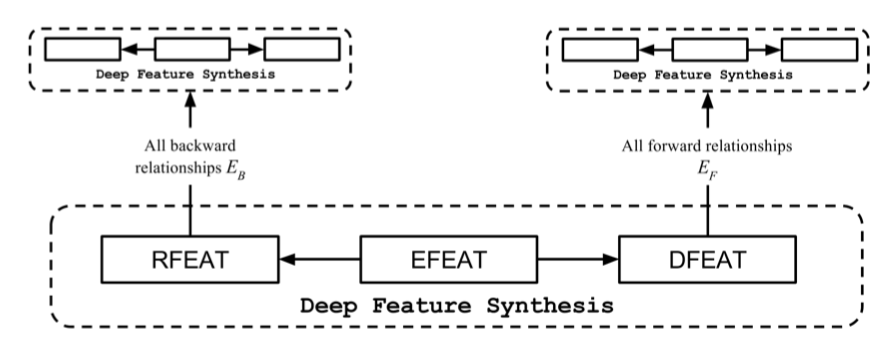
각 피처 유형을 합성할 때 계산 제약 조건의 그림. rfeat 및 dfeat 피처는 독립적으로 합성할 수 있는 반면, efeat 피처는 rfeat 및 dfeat 피처에 의존합니다. 심층 피처 합성을 위한 접근법의 한 가지 예는 알고리즘 1에 나와 있습니다.

다음으로 대상 엔터티와 관련된 엔터티에 자체 관련 엔터티가 있는 시나리오를 고려합니다. 이 경우를 처리하기 위해, 위에서 설명한 것과 동일한 순서를 사용하여 피처를 재귀적으로 생성할 수 있습니다. 재귀는 특정 깊이에 도달하거나 관련 엔터티가 없을 때 종료될 수 있습니다.

알고리즘 1

위의 MAKE_FEATURES 알고리즘 의사 코드는 $i$ 번째 엔터티를 위한 피처 $F^i$ 를 만듭니다. 재귀 호출의 구성 및 각 피처 유형의 계산은 위에서 설명한 제약 조건을 따릅니다. 의사 코드의 RFEAT, DFEAT 및 EFEAT 함수는 제공된 입력을 기반으로 각 피처 유형을 합성합니다. 알고리즘은 합성된 피처를 나중에 사용하는 것을 돕기 위해 정보를 저장하고 반환합니다. 이 정보에는 피처 값뿐만 아니라 적용된 기본 피처 및 피처에 대한 메타 데이터도 포함됩니다.

우리 알고리즘에서는 ffeat 피처와 rfeat 피처 사이 제약이 없더라도, ffeat 전에 rfeat을 계산하도록 선택했습니다. 또한 $E_V$는 우리가 “방문한” 엔터티를 추적합니다. 10 행은 방문한 엔터티에 대한 dfeat 피처가 포함되지 않도록 합니다. 이것은 불필요한 피처를 계산하지 않도록 합니다. 예를 들어, 전자상거래 데이터베이스 예에서 Customer 엔터티의 피처를 작성하는 경우를 생각해봅시다. 주문한 고객의 연령에 따라 각 주문에 대해 dfeat을 작성하는 것은 이치에 맞지 않습니다. 나중에 Customer 를 위해 rfeat 을 만들 때 주문한 고객을 기준으로 각 주문을 집계하고, 각 그룹의 주문은 dfeat 피처에 대해 동일한 값을 갖기 때문입니다.

그림 4

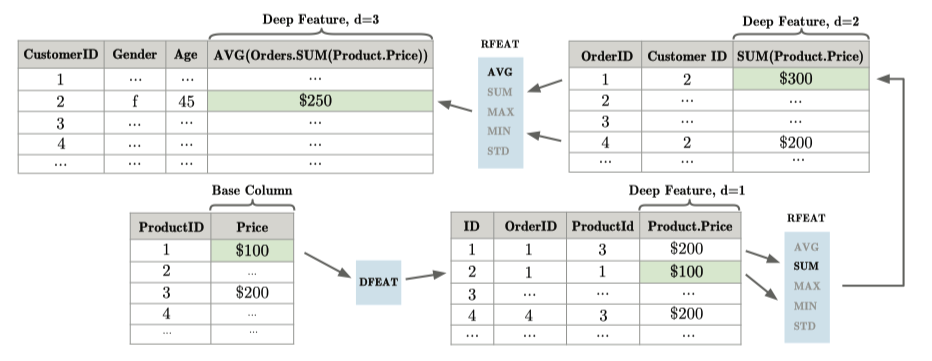
그림 4. 심층 피처 합성에 의해 생성 될 수 있는 피처의 예. 그림은 엔터티 간 관계를 순회하여 피처가 서로 다른 깊이에서 계산되는 방법을 보여줍니다.

그림 4는 재귀적으로 생성되는 피처의 예를 보여줍니다. 이 예에서는 결국 모든 고객의 평균 주문 크기를 계산합니다. 그러나 이 값을 실현하기 위해 Product 엔터티부터 시작하여 중간 계산을 수행합니다. 먼저, 제품 가격을 ProductOrders 엔터티에 추가하기 위해 dfeat 피처를 계산합니다. 다음으로 Orders 엔터티의 특정 인스턴스와 관련된 모든 ProductOrders 인스턴스에 SUM 함수를 적용하여 주문에 대한 rfeat 피처를 계산합니다. 마지막으로, 우리는 각 고객의 평균 총 주문 크기를 계산하기 위해 또 다른 rfeat 피처를 계산합니다.

D. 피처 수의 증가

심층 피처 합성에서는 열거할 수 있는 피처 공간이 매우 빠르게 커집니다. 그것이 어떻게 성장하는지 이해하기 위해, 우리는 주어진 엔터티에 대해 알고리즘이 합성할 피처의 수 $z$ 를 분석하겠습니다. 피처 합성의 재귀적 피처로 인해, 엔터티에 대해 생성된 피처 수는 관련 엔터티에 대해 생성된 수에 따라 다릅니다. 따라서 우리는 어느 엔터티에 대해 $i$ 번 재귀해 생성한 피처의 수를 $z_i$ 로 표시할 수 있습니다. 또한 데이터 세트의 모든 엔터티가 $O(j)$ 피처로 시작하고 $O(n)$ 순방향 관계와 $O(m)$ 역방향 관계가 있다고 가정합니다.

먼저, $O(m)$ 엔터티에 대한 rfeat 유형 피처를 합성합니다. 만약 우리가 $O(r)$ 개의 rfeat 함수가 있다고 가정한다면, 우리는 각각의 $m$ 엔터티에 대한 $O(r \cdot z_{i-1})$ 피처를 역방향 관계로 총 $O(r \cdot z_{i-1} \cdot m)$ 개의 부가 피처가 합성됩니다. 다음으로, 순방향 관계에서 엔터티의 모든 피처에 대해 하나의 dfeat 피처를 작성합니다. 이것은 $O (z_{i-1} \cdot n)$ 피처를 추가한다는 의미입니다. 마지막으로, 우리는 $j$ 개의 오리지널 피처와 새로 합성된 $O (z_{i-1} \cdot (r \cdot m + n))$ 피처를 사용하여 efeat 피처를 만들어야 합니다. 우리는 $O(e)$ 개의 efeat 함수가 있다고 가정합니다. 따라서 추가적인 $O (e \cdot j + e (z_{i-1} \cdot (r \cdot m + n)))$ efeat 피처를 합성합니다.

모든 rfeat, dfeat 및 efeat 피처를 결합하면 $z_i = O(z_{ i-1} \cdot (r \cdot m + n) (e + 1) + e \cdot j)$임을 알 수 있습니다. $z0$ 에서는 efeat 함수만 계산할 수 있으므로, $z_0 = O (e \cdot j)$입니다. $p = (r \cdot m + n) (e + 1)$ 이고 $q = e \cdot j$ 라고 하면, 대체하여 다음을 얻습니다.

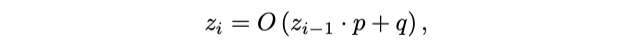
그리고 $z_{i-1}$을 $z_{i-2} \cdot p + q$ 로 대체합니다.

$z_0$ 까지 확장을 계속하면

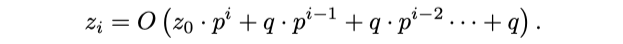
위의 방정식에서 $z_0 = O (e \cdot j) = q$ 를 대입하면 다음과 같습니다.

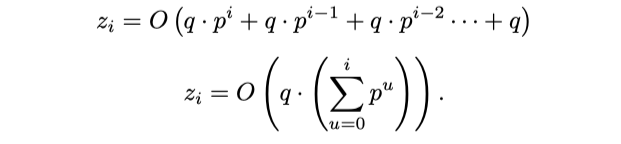
따라서, $z_i$에 대한 닫힌 형태는

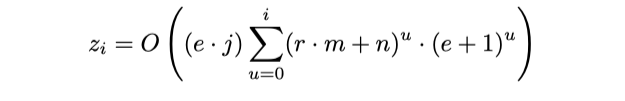
III. 심층 피처 합성: 구현

심층 피처 합성 을 구현하면서, 우리는 신속하게 데이터 과학 머신을 배포하고 새로운 데이터 세트가 발생할 때 합성된 피처를 평가하는 것을 목표로 했습니다.

데이터 과학 머신과 함께 제공되는 심층 피처 합성 알고리즘은 테이블용 InnoDB 엔진을 사용하여 MySQL 데이터베이스 위에 구축됩니다. 모든 원시 데이터 세트는 데이터 과학 머신에서 처리하기 위해 수동으로 MySQL 스키마로 변환되었습니다. 파이썬에서 합성된 피처를 계산, 관리 및 조작하기 위한 로직을 구현합니다.

데이터를 저장하는 방법과, 심층 피처 합성 의 요구 사항 사이의 자연스러운 병렬 관계로 인해 관계형 데이터베이스를 사용하기로 선택했습니다. 각 항목에서 엔터티는 테이블로 표시되고 피처는 열로 표시됩니다.

모든 수학 함수는 피처 함수 인터페이스를 제공해야합니다. 피처 함수는 피처 유형에 따라 하나 또는 두 개의 엔터티를 입력으로 사용합니다. 관계형 레벨 피처 및 소스가 다른 엔터티인 직접 피처의 경우 두 개의 엔터티가 필요합니다. 함수 정의는 관계에서 적용 가능한 열을 결정하고, 출력 값을 계산하는 방법을 책임집니다.

성능상의 이유로 데이터 과학 머신은 MySQL에서 제공하는 함수 위에 피처 함수를 빌드합니다. 현재 데이터 과학 머신은 AVG(), MAX(), MIN(), SUM(), STD() 및 COUNT()와 같은 rfeat 함수를 구현합니다. 또한 시스템은 텍스트 필드의 문자 수를 계산하는 length(), 날짜를 발생한 요일 또는 월로 변환하는 WEEKDAY() 및 MONTH()와 같은 efeat 함수를 구현합니다. 단순함에도 불구하고 이 작은 함수 기반은 데이터 과학 머신 평가에 사용할 수 있는 광범위한 피처를 작성하기에 충분합니다.

필터 객체는 rfeat 함수에 대한 데이터의 하위 집합을 선택할 수 있는 유연한 방법을 제공합니다. “and” 또는 “or”과 같은 논리 연산자를 사용하여 기존 필터 개체를 결합하여 새로운 필터 개체를 만들 수 있습니다. 필터 개체는 필터링되는 열을 반환하는 인터페이스와, MySQL 쿼리에 직렬화하는 방법을 제공합니다.

필터 객체는 심층 피처 합성 에 유용한 두 가지 기능을 구현합니다. 첫째, 특정 조건이 참인 경우에만 rfeat 함수를 적용하는 방법을 제공합니다. 우리는 이 사용법을 범주형 필터 라고 부릅니다. 예를 들어 “X 회사가 제조한 제품에 이 고객이 지출한 총 금액”은 범주형 필터로 구성됩니다. 둘째, 날짜 피처를 구성할 수 있습니다. 예를 들면 “고객이 3월 31일 이후, 4월 30일 이전에 주문한 주문의 수”.

데이터 과학 머신은 필요할 때만 데이터베이스 쿼리를 만듭니다. 기능을 계산하는데 필요한 데이터는 여러 테이블에 저장될 수 있으므로, 쿼리의 SELECT 절 또는 WHERE 절에 있는 모든 열에 액세스 할 수 있도록 테이블을 조인해야 합니다. 쿼리 예는 그림 5에 있습니다. 쿼리는 조인과 테이블 스캔 수를 줄이기 위해 한 번에 여러 계산을 수행하도록 최적화되었습니다.

그림 5

그림 5. KDD cup 2014 데이터 세트에서 Donors 엔터티에 대한 피처를 작성하기 위해, 데이터 과학 머신에서 자동 생성된 MySQL 쿼리의 예. 이 쿼리는 각 공여자가 제공한 총 금액을 계산합니다.

IV. 예측 기계 학습 경로

심층 피처 합성 에서 만든 피처를 사용하기 위해, 일반화된 기계 학습 경로를 구현합니다.

첫 번째 단계는 예측 문제를 공식화하는 것입니다. 모델링할 데이터 세트의 피처 중 하나를 선택하여 이를 수행합니다. 여기서 예측하고자 하는 피처를 목표 값으로 부릅니다.

목표 값을 선택한 후 예측에 사용하기에 적합한 피처들을 결합합니다. 이러한 피처들을 예측 변수(predictors) 라고 합니다. 예측 변수가 공통 기본 데이터를 목표 값으로 하여 계산되거나, 목표 값이 발생할 때 존재하지 않는 데이터에 의존하는 경우, 유효하지 않은 것으로 필터링됩니다. 또한 데이터 과학 머신은 각 엔터티 피처와 관련된 메타데이터 데이터베이스를 관리합니다. 이 메타데이터 에는 피처를 구성하는 데 사용된 원래 데이터베이스의 기본 필드에 대한 정보와, 그 안에 포함된 시간 종속성이 포함되어 있습니다.

재사용 가능한 기계 학습 경로

목표 피처와 예측 변수를 선택하면 데이터 과학 머신은 데이터 전처리, 피처 선택, 차원 축소, 모델링 및 평가를 위한 초모수화된 경로를 구현합니다. 초모수를 튜닝하기 위해 데이터 과학 머신은 지능형 초모수 최적화를 수행하기 위한 도구를 제공합니다. 기계 학습 및 예측 모델 구축을 위해 다음 단계가 수행됩니다.

데이터 전처리 : 머신 러닝 경로에 들어가기 전에 null 값을 제거하고, 원핫 인코딩을 사용하여 범주형 변수를 변환하고, 피처를 정규화하여 데이터를 정리합니다.

피처 선택 및 차원 축소 : 심층 피처 합성 은 엔터티 당 많은 수의 피처를 생성합니다. 피처 공간의 크기를 줄이기 위해 두 가지 기술을 순차적으로 사용합니다. 먼저, 절단 SVD 변환을 사용하고, SVD의 $n_c$ 구성 요소를 선택합니다. 그런 다음 목표 값에 대한 f-value 값을 계산하여 각 SVD 피처의 순위를 정하고, 상위 $\gamma\%$ 피처를 선택합니다.

모델링 : 모델링을 위해 $n$ 개의 의사 결정 트리를 구성하여 랜덤 포레스트를 사용합니다. 각 의사 결정 트리의 깊이는 $m_d$이며 $\beta$로 표시되는 피처의 일부를 사용합니다. 많은 데이터 세트의 경우, 서로 다른 데이터 포인트 클러스터에 대해 별도의 모델을 갖는 것이 강력할 수 있습니다. 이를 이용하기 위해 우리는 K-Means 를 사용해 훈련 포인트를 $k$ 클러스터로 분리하고, 각 군집에 대해 별개의 랜덤 포레스트를 훈련시킵니다. 테스트 샘플에 대한 라벨을 예측하기 위해, 훈련된 클러스터 분류기는 데이터 포인트에 클러스터 라벨을 할당한 다음 해당 모델을 적용합니다.

경우에 따라 분류 문제에서 목표 값 클래스 중 하나가 제대로 표시되지 않습니다. 이를 보완하기 위해 모델링 단계에서는 표현이 부족한 클래스를 $rr$ 계수로 다시 가중치를 지정할 수 있습니다.

모델링 단계에서는 $n$, $m_d$, $\beta$, $k$, $rr$ 의 네 가지 모수를 소개했습니다. 다음으로 이 경로를 자동 튜닝하는 방법을 설명합니다.

V. 가우시안 코퓰라 프로세스를 이용한 베이지안 모수 최적화

머신 러닝 파이프 라인의 여러 단계에는 튜닝할 수 있는 모수가 있으며, 이 튜닝은 모델 성능에 현저한 영향을 줄 수 있습니다. 순진한 그리드 검색은 가능한 모든 모수 값 조합을 고려할 경우 6 x 490 x 90 x 10 x 450 x 20 x 100 = 2,381,400,000,000 (2조 3천 8백 14억)의 가능성 공간에서 검색을 초래합니다. 이 공간의 탐색을 돕기 위해 가우시안 코퓰라 프로세스(Gaussian Copula Processes, GCP)를 사용합니다. GCP는 모수 선택과 전체 경로의 성능 간의 관계 $f$ 를 모델링하는 데 사용됩니다 (모델). 그런 다음 새 모수를 샘플링하고 그 성능을 예측합니다 (샘플). 마지막으로 선택 전략을 적용하여 다음에 사용할 모수를 선택합니다 (최적화). 아래에서 각 단계를 자세히 설명합니다.

모델 : 일반적으로 가우시안 프로세스는 $f$ 가 $\chi, {f(\tilde p_i)}^N_{i=1}$에서 유한 집합 $N$ 포인트 $\bar p_{1 \dotso n}$ 에서 $\mathbb R^N$ 다변량 가우시안 분포가 되도록 모델링하는 데 사용됩니다. 이러한 공정의 속성은 평균 함수 (중앙형 데이터의 경우 일반적으로 0으로 간주)와, 공분산 함수 $K \colon P \times P \rightarrow \mathbb R$ 로 결정됩니다.

이 논문에서 우리는 Wilson et al.에 의해 정의 된 코퓰라 프로세스에 기반해 출력 공간의 비틀림(warping) 을 통한 파라미터 최적화를 위한 새로운 접근법을 소개합니다. GCP에서, $f (\bar p_i) _ {i = 1}^N$ 의 다변량 분포를 모델링하기 위한 가우스 프로세스 대신, ${f (\bar p_i) _ {i = 1}^N}$ 를 ${\Psi \circ f(\bar p_i)} _ {i=1}^N$ 으로 변환하는 $\Psi \colon \mathbb R \rightarrow \mathbb R$ 맵핑을 한 후, 가우시안 프로세스로 모델링됩니다. 이를 통해 각 $f (\bar p)$에 대해 가정된 가우스 주변 분포를 보다 복잡한 것으로 변경합니다.

매핑 함수 : 참조 5에서, 변환된 출력이 가우시안 프로세스에 의해 가장 잘 모델링되도록 모수화된 매핑이 학습됩니다. 그러나 이러한 매핑은, 동일한 데이터 세트에 대한 많은 실험에서 다른 매핑을 학습하기에 불안정합니다. 더욱이 유도된 일변량 분포는 거의 대부분 가우시안(정규 분포)이며, 모수화된 매핑은 더 큰 유연성을 제공할 수 없었습니다. 이를 극복하기 위해 커널 밀도 추정을 통해 관찰된 데이터에서 주변 분포를 학습하는 새로운 접근 방식을 사용합니다. 보다 구체적으로, 파라미터 $\bar p = {p_1 \dotso p_m}$ 및 성능 함수 $f (\bar p)$를 고려하겠습니다. 변환의 첫 번째 단계는 커널 밀도 추정기를 사용하여 ${f (\bar p_i)} _ {i = 1}^N$ 의 밀도를 모델링한 다음, 이 밀도의 cdf 를 추정합니다. 그런 다음 ${f (\bar p_i)} _ {i = 1}^N$ 의 각 값에 대한 cdf 값을 생성하는데, $g=cdf(f(\bar p))$ 로 나타냅니다. $g$ 가 표준 정규 분포에서의 표본이라고 가정하면, $g$ 의 값에 $\psi^-1$을 적용하여 $h = \psi^-1 (g)$로 주어지는 최종값을 생성합니다. $h$ 는 정규 가우스 프로세스를 사용하여 모델링하려는 $f (\cdot)$의 변환을 나타냅니다. 따라서 가우시안 프로세스 모델링에 대한 입력 값은 $\bar p_{1 \dotso n}$ 및 대응하는 $h_{1 \dotso n}$ 값입니다.

공분산 함수 맞추기 : 참조 3의 119-221 페이지에서 영감을 얻은 주기적 성분을 갖는 제곱 지수의 일반화를 사용합니다. 우도 최대화를 통해 모델 모수를 학습합니다.

샘플링 : $\mathcal P$ 에서 반복적으로 포인트를 샘플링하고 GCP 모델을 사용하여 해당 결과 값 $f(\bar p)$ 를 예측한 후, 다음에 선택할 포인트를 결정합니다.

최적화 : 이 최종 단계는 일반적으로 획득 함수 $a$ 를 최대화하여 수행됩니다. 이 함수에 대한 입력은 탐색 (exploration, 입력 공간 $\mathcal P$ 의 탐색되지 않은 영역의 테스트 포인트) 과 활용 (exploitation, 높은 $f (\bar p)$ 값을 예측하는 테스트 포인트) 간의 균형을 맞추기 위해 $f$에서 파생됩니다. 특히 이것으로 인하여 국소 최적값 근처 검색에 집중하지 않아도 됩니다. 그러므로 주어진 관측치 $(p_{1 \dotso n}, f(p_n))$ 에 대해, $\mathcal P$ 에서 ${\bar p}_i^\prime$ 을 임의 표집하고, 그것의 출력 $f_i^\prime$ 을 예측하고, $a$ 를 최대화하는 $\bar p^{\prime \star}$ 를 선택합니다.

VI. 실험 결과

데이터 과학 머신은 이런 방식의 최초이기에 “기계 성능은 어느 정도입니까?”, “중요한 피처를 생성했습니까?” 및 “자동화가 잘 동작합니까?” 같은 질문들을 언급하려 합니다. KDD cup 2014, IJCAI 및 KDD cup 2015와 같은 많은 데이터 과학자들이 최고의 결과를 위해 경쟁하는 데이터 세트에 적용하여 데이터 과학 머신의 효과를 입증하였습니다. 이런 각 대회에서는 수백명의 데이터 과학 팬들이 주최자들에 의해 고안된 예측 문제 풀이에 참여합니다. 그림 6의 도표는 각 데이터 세트의 엔터티를 보여줍니다. 이어서 각 문제를 간략하게 설명하겠습니다.

그림 6

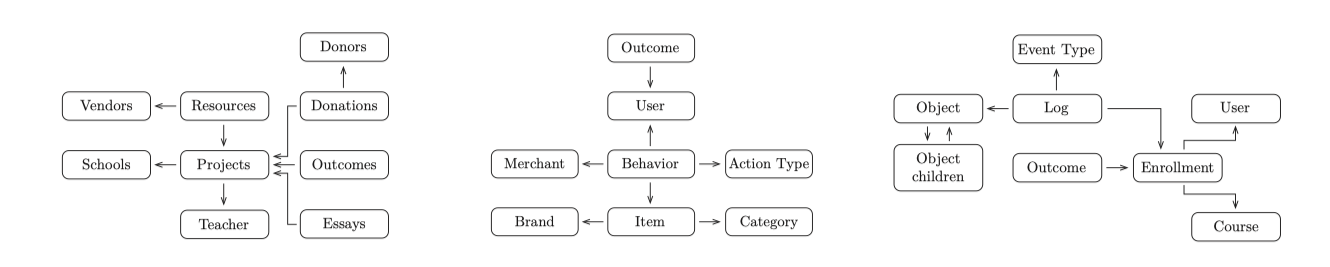
그림 6. 2014-2015 년 동안 왼쪽에서 오른쪽으로 KDD 컵 2014, IJCAI 및 KDD 2015 컵의 세 가지 다른 데이터 과학 경연 대회. 총 906 개의 팀이 이 대회에 참가했습니다. 데이터 과학 머신 솔루션의 예측이 제출되었으며 결과는 이 논문에 보고됩니다.

KDD cup 2014 - 프로젝트 흥분 : DonorsChoose.org의 과거 프로젝트 기록을 사용하여 크라우드 펀딩 프로젝트가 “흥분되는” 것인지 예측하십시오.

IJCAI - 반복 구매자 예측 : 과거 판매자 및 고객 쇼핑 데이터를 이용하여 판촉 기간 동안 구매한 고객이 반복 구매자로 전환되는지 예측하십시오.

KDD cup 2015 - 학생 이탈 : 온라인 과정에서 리소스와 학생의 상호 작용을 이용하여 향후 10일 내에 학생이 이탈할 것인지 예측합니다.

그림 7

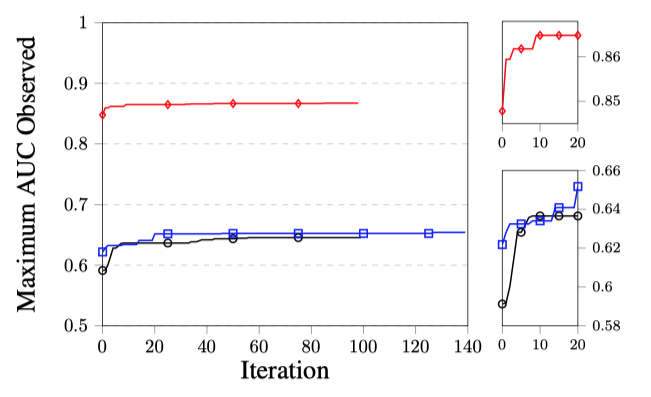
그림 7. 세 가지 데이터 세트 모두에 대해 반복적으로 발견된 최대 교차 검증 AUC 점수. 위에서 아래로 : KDD 컵 2014, IJCAI, KDD 컵 2015

경쟁을 위해 데이터 과학자는 피처 엔지니어링, 모델링 및 미세 튜닝에 관여합니다. 데이터 과학 머신에서 이러한 세 가지 활동은, 초기 모수 설정외 최소한의 사람 개입으로 수행할 수 있어 계산 한계가 최대화됩니다. 우리는 데이터 과학 머신에서 완전 자동화된 피처 생성 (심층 피처 합성)을 먼저 실행했습니다. KDD 컵 2014의 경우 시간 간격 피처도 구성했으며 IJCAI 및 KDD 컵 2015의 경우 몇 가지 범주형 필터를 만들었습니다. 심층 피처 합성 을 실행 한 결과는 표 3에 나와 있습니다.

표 3

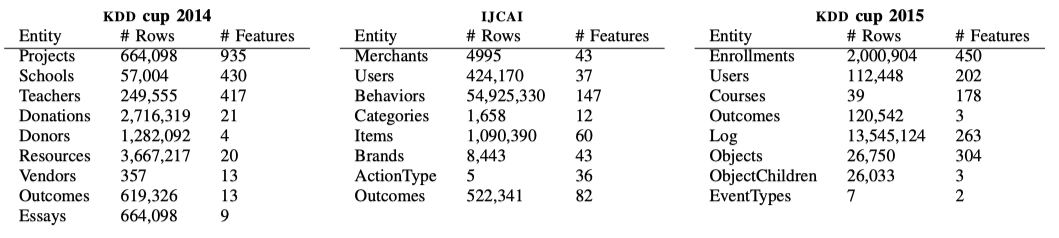
표 3. 각 데이터 세트의 엔터티 당 행 수 및 합성 피처의 수입니다. KDD CUP 2014, IJCAI 및 KDD CUP 2015의 압축되지 않은 크기는 각각 3.1GB, 1.9GB 및 1.0GB입니다.

머신 러닝 경로에 대한 최적의 모수를 결정하기 위해 데이터 과학 머신은 가우스 코퓰라 프로세스 기반 튜닝을 실행합니다. 최적 수행의 모수는 표 1에 표시되어 있습니다.

표 1

표 1. 머신 러닝 파이프 라인의 모수 요약과, 데이터 세트에 GCP를 실행하여 얻는 최적값.

튜닝을 사용하거나 사용하지 않고 데이터 과학 머신을 실행한 결과는 표 2에 나와 있습니다.

표 2

표 2. 데이터 과학 머신이 달성한 AUC 점수. “기본”점수는 기본 모수를 사용합니다. “로컬” 점수는 K-Folds (K = 3) 교차 검증의 결과이며, “온라인” 점수는 컨테스트 예측 제출에 기반을 두고 있습니다.

데이터 과학 머신과 인간의 능력을 어떻게 비교할지에 도움이 되도록 실험 결과와 대회들의 공개 성능을 비교합니다. 표 4는 데이터 과학 머신이 리더 보드의 다른 경쟁자와 비교했을 때의 결과를 보여줍니다. 이 표에는 데이터 과학 머신을 이긴 팀과 진 팀에 대한 기본 정보가 있습니다.

표 4

표 4. 데이터 과학 머신과 인간의 노력을 비교. IJCAL의 제출 수에 대한 데이터는 없음.

그림 8은 데이터 과학 머신의 점수가 순위표의 각 백분위 수에서 다른 경쟁자와 어떻게 비교되는지 보여줍니다. 다음 섹션에서는 이 결과에 대한 해석을 제시합니다.

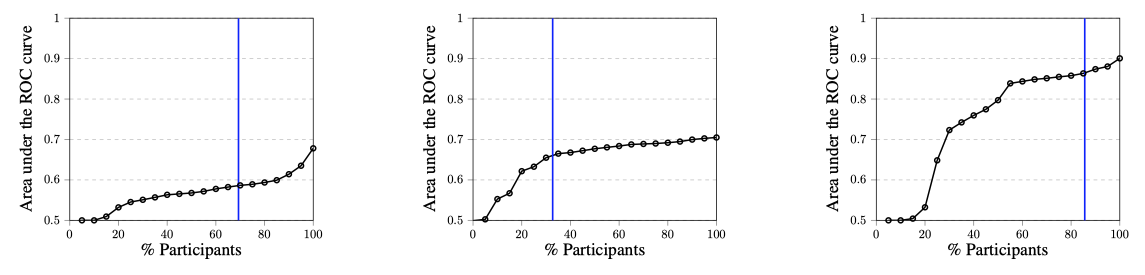
그림 8. AUC 점수와, 그것을 달성한 참가자의 %. 수직 선은 데이터 과학 머신을 표시. 왼쪽부터 KDD CUP 2014, IJCAI, 그리고 KDD CUP 2015

VII. 논의

이 섹션에서는 세 가지 데이터 세트 모두의 결과가, 데이터 과학자를 모사하는 데 있어 데이터 과학 머신의 효과를 어떻게 반영하는 지에 대해 논의합니다.

귀중한 합성 피처 만들기 : 3 개 대회 중 2 개 대회에서 데이터 과학 머신은 모든 경쟁자가 달성 한 최고 점수의 90% 이상을 달성했습니다. KDD 15에서 최고의 성능으로 다른 경쟁자의 약 86% 를 이겼습니다. 합성 된 피처가 가치가 없다면, 우리는 세 가지 경쟁에서 데이터 과학 성능이 그렇게 잘 수행 될 것으로 기대하지 않을 것입니다. 이 결과는 과학적으로 가치가 있는 새로운 피처를 생성할 수 있음을 보여줍니다.

데이터 과학 머신이 가장 적은 수의 경쟁자를 이긴 IJCAI 경쟁에서도 기계는 인간 지능으로 수집되는 것과 유사한 문제에 대한 정보를 포착했습니다. 대회 기간 동안 스폰서는 벤치 마크 모델을 발표했습니다. 제안된 모델은 해당 판매자와 유사한 상점에서 고객의 이력을 사용하여 예측했습니다. 이를 위해 판매자 유사성을 측정하는 한 가지 방법을 제안했습니다. 후원자들은 이 방법이 적어도 .65의 AUC를 달성 할 것이라고 주장했습니다. 이는 데이터 과학 머신 GCP 최적화 솔루션이 .66 이상의 AUC를 달성했기 때문에 주목할 만합니다. 이는 데이터 과학 머신이 최소한 사람이 제안한 모델만큼 좋은 모델을 자동으로 도출할 수 있음을 의미합니다. 또한 경쟁자의 등급이 올라갈 때 개선율을 보면 데이터 과학 머신의 점수는 점수 개선이 평평해지는 지점에 있습니다 (그림 8 참조). 데이터 과학 머신은 0.6606의 AUC를 달성한 반면 최고 경쟁자의 AUC는 0.704로 약 0.04의 차이를 나타 냈습니다. 이는 데이터 과학 머신에서 선택한 피처가 데이터 세트의 주요 측면을 포착했으며, 사소한 개선 사항만 놓쳤음을 나타냅니다.

다른 두 대회에서는 데이터 과학 머신의 피처가 KDD 15에서 86%, KDD 14에서 70%로 대다수의 경쟁자를 이길 수 있을 정도로 충분했습니다. KDD 15에서 데이터 과학 머신은 점수 향상의 정점에 도달하여 최고 점수는 0.8621이며 최고 경쟁자는 0.90이었습니다.

이는 데이터 과학 머신에 의해 합성된 피처가 예측 문제의 중요한 측면을 포착한다는 우리의 말을 증명합니다. KDD 14에서 데이터 과학 머신이 선택한 피처는 대부분의 경쟁자보다 성능이 우수하지만, 개선 속도가 안정되지 않기에 최고의 경쟁자에는 미치지 못합니다.

자동 튜닝 효과 : 앞에서는 데이터 과학 머신이 가치있는 피처를 생성하는지에 대해 설명했습니다. 데이터 과학 머신의 또 다른 중요한 작업은 사용할 피처 선택 후 해당 피처를 가장 잘 사용하도록 모델을 튜닝하는 방법을 선택하는 것입니다. 자동 튜닝을 사용하여 데이터 과학 머신은 로컬 및 온라인의 세 가지 데이터 세트 모두에서 점수를 높일 수 있었습니다 (표 2 참조). 이 프로세스를 통해 데이터 과학 머신은 기본 모수에 의존하지 않고 다양한 문제에 적응할 수있는 기계 학습 경로를 설계할 수 있습니다.

KDD 15 데이터 세트에 대한 온라인 예측 제출은 기본 모수와 함께 자동 튜닝을 사용하는데 대한 흥미로운 통찰력을 제공했습니다. 기본 모수를 사용하면 로컬 교차 유효성 검사 점수가 좋은 결과를 가져 오는 것 같습니다. 그러나 예측이 경쟁 웹 사이트에 업로드될 때 결과는 로컬에서 찾은 것만 큼 좋지 않았습니다. 훈련 설정에 문제가 있는 것으로 의심되어, 문제를 해결하기 위해 데이터 과학 머신에서 생성 한 450 개의 피처를 수동으로 검사하고 많은 머신 러닝 경로 모수 초기화를 테스트했습니다. 우리가 개발한 인터페이스를 사용하여 훈련 경로 자체가 아닌 기본 모수에 문제가 있다고 결론을 내릴 수 있었습니다.

우리가 수행 한 프로세스는 실무 데이터 과학자의 프로세스와 유사합니다. 먼저 시스템에 포함할 피처를 실험한 다음 기계 학습 프로세스의 모수를 실험했습니다.

이는 데이터 과학 머신에서 채택한 자동 튜닝 프로세스에, 위에서 설명한 문제가 발생하지 않았으며 피처를 선택하고 모수를 튜닝할 때 KDD 15의 경쟁자와 비교하여 성능이 우수했기 때문에 주목할 만합니다. 이는 데이터 과학 머신의 모수 튜닝 방식이 작업 흐름에서 몇 시간의 디버깅을 제거했음을 의미합니다. 또한 머신 러닝 알고리즘에 대한 기본 모수 선택의 어려움을 잘 보여줍니다. 자동 튜닝 프로세스가 없으면 데이터 과학 머신은 목표를 달성하지 못했을 것입니다.

인간의 가치 : 데이터 과학 머신은 “전문가”를 다른 사람보다 우선시하는 통찰력을 얻지 못한 경쟁자에 비해 성능이 우수합니다. 데이터 과학 머신이 평지의 끝을 향해 득점하는 그림 8에서 이를 확인할 수 있습니다. 때로는 리더 보드 위로 올라가는 데 필요한 비용이 적절하지 않을 수도 있습니다. 리더 보드 위로 올라가려는 인간의 노력은 그림 9와 같습니다.

그림 9

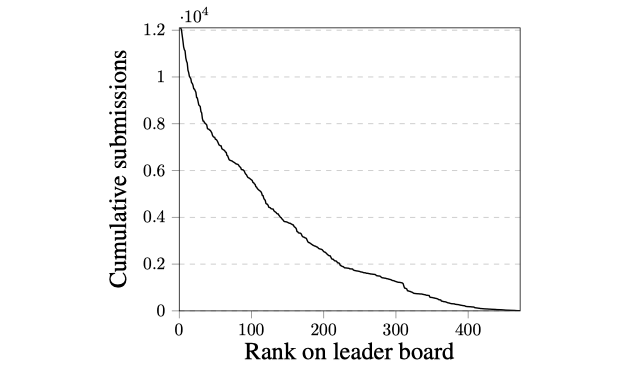
그림 9. KDD 컵 2014에서 각 리더 보드 순위에 제출된 누적 제출 수. 리더 보드 위로 올라갈수록 경쟁자가 제출한 총 제출 수가 기하 급수적으로 증가한 것을 볼 수 있습니다.

데이터 과학자를 위한 시사점 : 데이터 과학 머신의 경쟁력있는 성공은 데이터 과학자와 함께 역할을 수행할 것을 제안합니다. 현재 데이터 과학자는 피처 생성 및 선택 프로세스에 깊게 관여합니다. 우리의 결과는 데이터 과학 머신이 가치있는 피처를 자동으로 생성하고 해당 피처를 사용하여 모델을 만드는 방법을 알아낼 수 있음을 보여줍니다. 인간이 모든 데이터 세트에서 데이터 과학 머신을 이기기는 하지만, 이 기계의 가성비는 데이터 과학에 적합한 장소가 있음을 시사합니다.

먼저, 데이터 과학 머신을 사용하여 벤치 마크를 설정할 수 있습니다. IJCAI 주최자가 경쟁자들이 참고로 사용할 벤치 마크를 발표한 것처럼, 데이터 과학 머신은 데이터 과학자 실습을 위한 성능 레퍼런스가 될 수 있습니다. 데이터 과학 머신 성능이 과제의 목적에 적합한 경우 추가 작업이 필요하지 않습니다. 주어진 데이터 세트가 데이터 과학 기계에서 이익(gain)을 달성하고, 추가적인 인간의 작업이 한계 수익을 감소시키는 KDD 15 또는 IJCAI와 유사한 경우 많은 시간을 절약할 수 있습니다. 추가 이익이 중요한 KDD 14의 경우에도 높은 비용이 드는 것으로 보입니다. 데이터 과학 머신을 사용하면 예측 문제를 모델링하는 데 소요되는 시간을 크게 줄일 수 있습니다.

둘째, 데이터 과학 머신은 데이터 과학의 창의성을 키울 수 있습니다. 데이터 과학 머신은 최상의 피처를 찾기 위해 잠재적인 피처와 모델의 넓은 공간을 탐색하여 문제를 해결합니다. 데이터 과학자들은 종종 테스트할 수 있는 리소스보다 더 많은 아이디어를 고려해야 한다는 문제에 직면합니다. 데이터 과학 머신은 생성할 특성을 반복하지 않고, 잠재적인 피처를 열거하고 데이터 과학자가 피처 선택을 반복하도록 하여 이 문제를 해결하는 데 도움을 줄 수 있습니다. 이러한 방식으로 데이터 과학자는 데이터 과학 머신의 솔루션으로 시작한 뒤, 그들의 전문 지식을 이용해 그것을 개선할 수 있습니다.

haje01 노트

목차